The idea of using expected value estimates to to compare effective charitable interventions is not new. A few notable examples include Holden Karnofsky’s skeptical post in 2011, and detailed responses by Gregory Lewis in 2014 and Michael Dickens earlier this year. Even GiveWell, despite (repeatedly) cautioning against taking the approach too literally, maintains a cost effectiveness model, using staff input to compute a median effectiveness for each of its recommended charities.

In this post I’ll propose a framework for using techniques from modern portfolio theory to extend the expected value approach and minimize uncertainty in charitable giving.

So what’s the deal with expected value?

The main drawback of an expected value approach is that, by itself, it doesn’t say anything about the uncertainty of the estimate. This weakness is demonstrated by the Pascal’s mugging thought experiment, in which very unlikely outcomes have extremely high payouts. Holden, with the help of Dario Amodei, suggests resolving this issue using a Bayesian approach, starting with a prior distribution for estimated cost effectiveness, and updating it with a noisy measurement of the true effectiveness. While this type of Bayesian analysis is intuitively appealing, it’s still necessary to generate a reasonable prior, including both the expected value and uncertainty of cost effectiveness estimates.

Fermi estimation gets us part of the way there, and GiveWell’s spreadsheet is a good place to start. By decomposing the problem into a series of informed guesses that, when combined, yield an overall expected value, the seemingly overwhelming problem of comparing unrelated charitable interventions can at least be made approachable, if not intuitive. Unfortunately, this approach also lacks an estimate of uncertainty, and is still vulnerable to Pascal’s mugging.

The part where things get neat

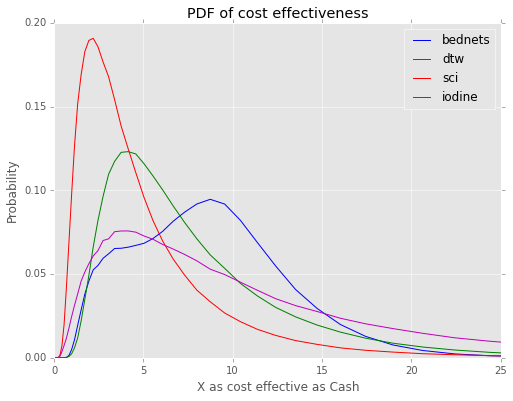
By treating the GiveWell staff responses as independent random variables, however, we can at least get a feel for the relative uncertainty associated with each intervention. To that end, I recreated the mid-2016 GiveWell cost effectiveness model in Python and ran a Monte Carlo simulation on it, randomly selecting a value from the staff pool for each variable on each iteration. The resulting probability distributions are shown below.

This is somewhat intuitively satisfying: top recommendations like bednets and deworming have a relatively low variance, while iodine has a somewhat wider spread. And because the estimates are (pretty much) log-normally distributed, techniques from post-modern portfolio theory can be used to create a low variance, high returns portfolios of charitable interventions. Treating the PDFs like returns from securities, and running through the basic PMPT calculations (assuming \(t = 5\) for downside risk) produces the following:

Theoretically modern portfolios

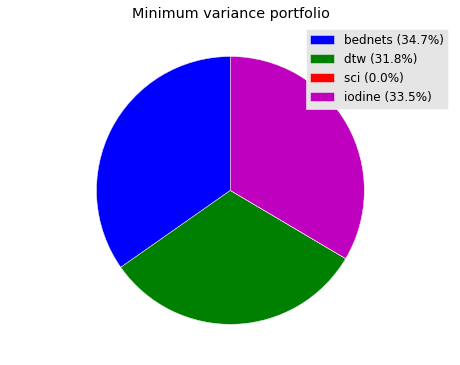
The minimum variance portfolio, or the combination of non-cash donations that produces the least downside risk, is shown here:

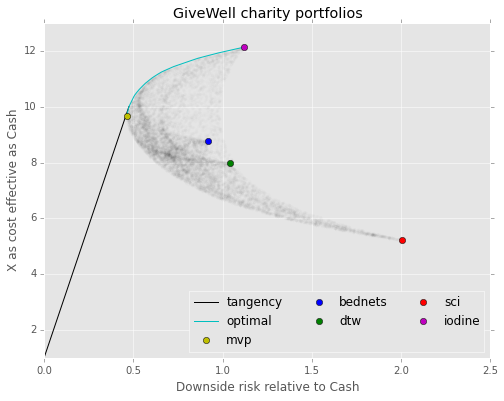
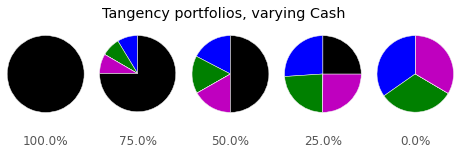
Arbitrarily lower downside risk can be achieved by combining cash donations with the tangency portfolio, as seen on the tangency line. A few example portfolios are shown below:

Higher returns are also possible, at the cost of increased risk, by moving right from the MVP on the optimal portfolio line. Since it’s impossible to short charities (I think?), this line terminates at the highest risk/reward intervention.

Where do we go from here?

The above analysis comes with the massive caveat that I’m not an expert in charity evaluation, portfolio theory, Bayesian statistics, etc. I don’t fully understand the majority of the inputs to GiveWell’s model, and I’m sure smarter people than me have spent longer thinking about this exact problem.

That being said, I do believe that stochastic Fermi estimation and portfolio theory can provide a useful framework for thinking about charitable giving under uncertainty. For instance, a sensitivity analysis over the variable space could highlight which model inputs deserve the most attention. I’m also interested in how ideas like crowdsourced intelligence and Bayesian networks might be used for generating more accurate inputs and intuitive models.